
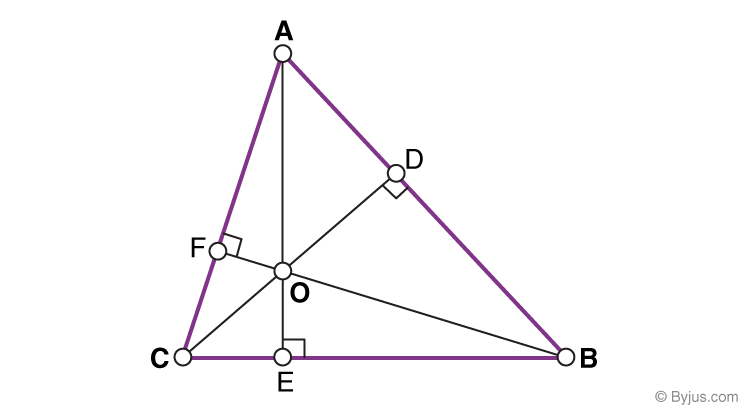
You would naturally pick the altitude or height that allowed you to ship your triangle in the smallest rectangular carton, so you could stack a lot on a shelf.Īltitude for side U D ( ∠ G) is only 4.3 c m. Think of building and packing triangles again.
ALTITUDE GEOMETRY DEF HOW TO
How to Find the Altitude of a TriangleĮvery triangle has three altitudes. To get the altitude for ∠ D, you must extend the side G U far past the triangle and construct the altitude far to the right of the triangle. To get that altitude, you need to project a line from side D G out very far past the left of the triangle itself. The altitude from ∠ G drops down and is perpendicular to U D, but what about the altitude for ∠ U? We can construct three different altitudes, one from each vertex.įor △ G U D, no two sides are equal and one angle is greater than 90 °, so you know you have a scalene, obtuse (oblique) triangle. The height or altitude of a triangle depends on which base you use for a measurement. How big a rectangular box would you need? Your triangle has length, but what is its height? Imagine you ran a business making and sending out triangles, and each had to be put in a rectangular cardboard shipping carton. Obtuse triangles - One interior angle is obtuse, or greater than 90 °Īn altitude is a line drawn from a triangle's vertex down to the opposite base, so that the constructed line is perpendicular to the base.Acute triangles - All interior angles are acute, or each less than 90 °.Oblique triangles break down into two types: Right - One right angle ( 90 °) and two acute angles.
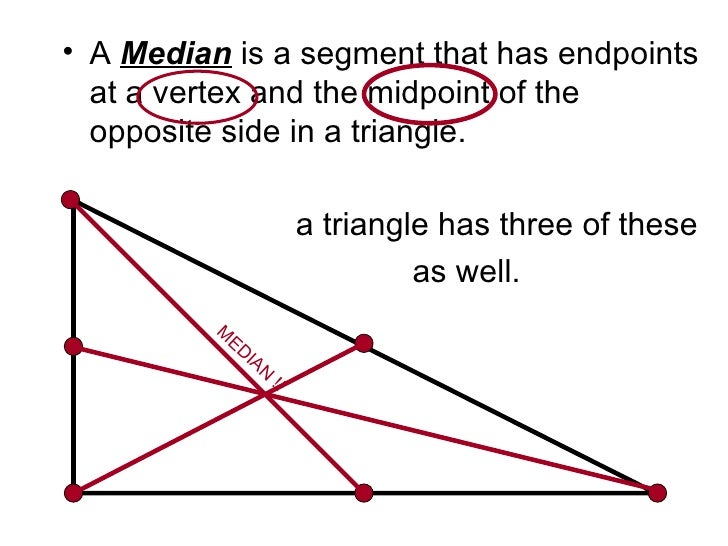
Anglesīy their interior angles, triangles have other classifications: Most mathematicians agree that the classic equilateral triangle can also be considered an isosceles triangle, because an equilateral triangle has two congruent sides.
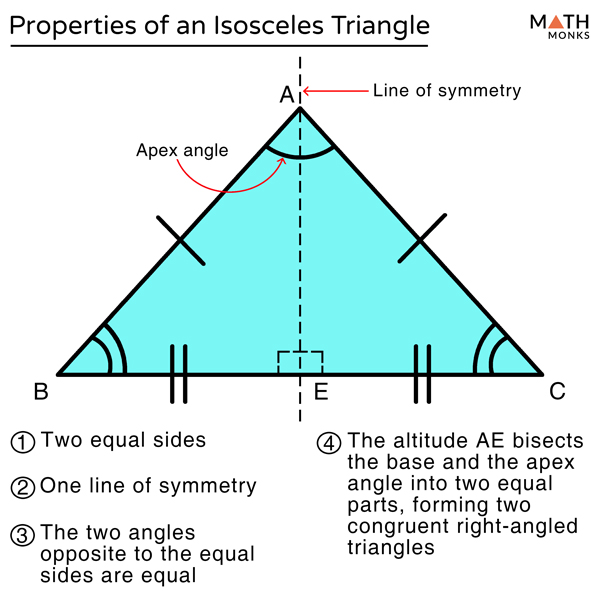
Locate the three altitudes for every type of triangle.Recognize and name the different types of triangles based on their sides and angles.Theorem 64: If an altitude is drawn to the hypotenuse of a right triangle, then it is the geometric mean between the segments on the hypotenuse.Įxample 1: Use Figure 3 to write three proportions involving geometric means.įigure 3 Using geometric means to write three proportions.Įxample 2: Find the values for x and y in Figures 4 (a) through (d).įigure 4 Using geometric means to find unknown parts.īecause it represents a length, x cannot be negative, so x = 12.After working your way through this lesson and video, you will be able to: This proportion can now be stated as a theorem. Theorem 63: If an altitude is drawn to the hypotenuse of a right triangle, then each leg is the geometric mean between the hypotenuse and its touching segment on the hypotenuse. These two proportions can now be stated as a theorem. This produces three proportions involving geometric means. Note that AB and BC are legs of the original right triangle AC is the hypotenuse in the original right triangle BD is the altitude drawn to the hypotenuse AD is the segment on the hypotenuse touching leg AB and DC is the segment on the hypotenuse touching leg BC.īecause the triangles are similar to one another, ratios of all pairs of corresponding sides are equal. They have been drawn in such a way that corresponding parts are easily recognized.įigure 2 Three similar right triangles from Figure (not drawn to scale). Theorem 62: The altitude drawn to the hypotenuse of a right triangle creates two similar right triangles, each similar to the original right triangle and similar to each other.įigure 2 shows the three right triangles created in Figure . The following theorem can now be easily shown using the AA Similarity Postulate. In Figure 1, right triangle ABC has altitude BD drawn to the hypotenuse AC.įigure 1 An altitude drawn to the hypotenuse of a right triangle.
Summary of Coordinate Geometry Formulas.Slopes: Parallel and Perpendicular Lines.Similar Triangles: Perimeters and Areas.Proportional Parts of Similar Triangles.Formulas: Perimeter, Circumference, Area.Proving that Figures Are Parallelograms.Triangle Inequalities: Sides and Angles.Special Features of Isosceles Triangles.Classifying Triangles by Sides or Angles.Lines: Intersecting, Perpendicular, Parallel.


 0 kommentar(er)
0 kommentar(er)
